First Draft
I hope to have another draft with drawings to help readability and visualization, especially considering the prominent use of color schemes below. I also would like to bring in some of the interactions I had with students between and during each step.
Description:
An illustration of the formal definition of a relation on a set as a subset of the cartesian product of , the cartesian product of with itself; equivalently, a relation on a set is an element of , the power set of the cartesian product of with itself.
To write out in what occurs on the board, we will let mean the yellow sticky note and use for the blue sticky note.
Ingredients in play
- sticky notes of two colors
- chalk and chalkboard
- care, creativity, and a lil bit of crazy (<–what others might say)
Step 0
What is important about defining a relation on a set and sharing that with anyone, students, math majors?
Step 1
Groups! Not yet those groups, but that could be part of the thinking process in Step 0. Each group of students names themselves and chooses a set name.
The set will comprise two elements, a sticky note of each color:
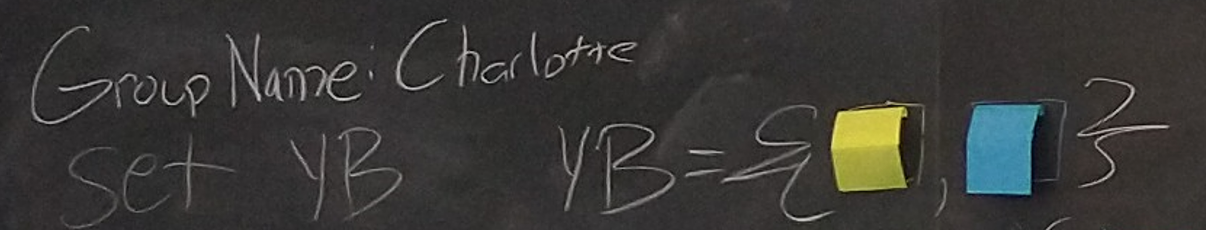
The Charlotte group named their set after the "yellow-blue" sticky notes.
Step 2
We now define the cartesian product of with :
Note that the cartesian product (notation: ) of set with set , whether and are the same set or distinct sets, is another set. The cartesian product of and is the set of all ordered pairs with a first entry from and second entry from : .
In our case, the set is playing the role of both and in the above description.
So we have
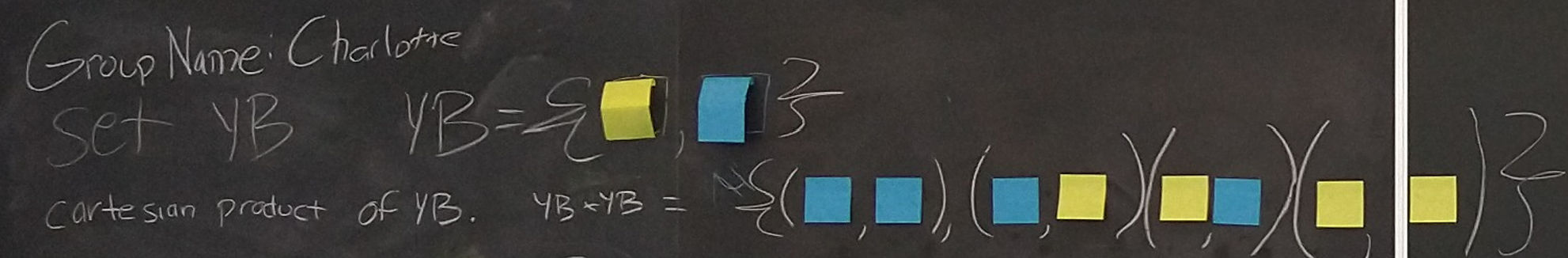
The Charlotte group then formed the cartesian product of the set they defined in Step 1.
Step 3
We now define the power set of the cartesian product :
The power set of a set is another set, truly. It contains all subsets of set . In our case, plays the role of :
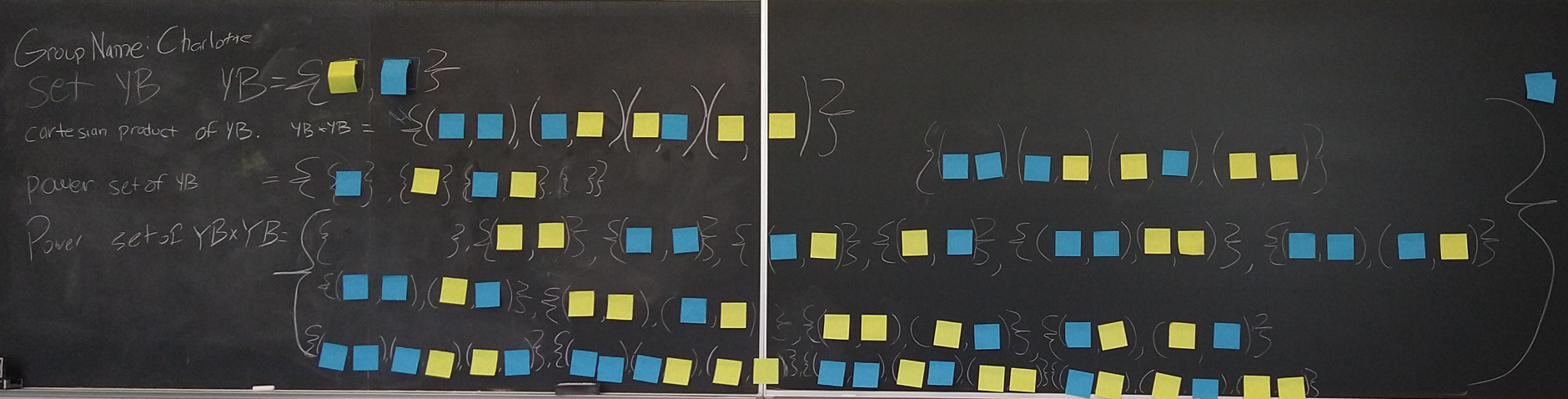
The Charlotte group then formed the power set of . The last subset containing all ordered pairs is not pictured.
Step 4
A relation on the set is an element of . In other words, a relation on a set is a subset of ; thus, a relation on a set is a set of ordered pairs with both entries from . Note: We can define a relation between two sets and by constructing and choosing an element (which is a subset of ).
Remarks
The empty set in Step 3 corresponds to the empty relation on .
Writing means . “The element is related to the element .”
Notation can help point to commonly used relations, emphasizing that relations allow us to formally analyze two elements of a set:
- “equal” relation on a set with notation
- “not equal” relation on a set with notation
- “less than” relation on with notation
- “less than or equal to” relation on with notation
- “greater than” relation on with notation
- “greater than or equal to” relation on with notation
Definition of a binay relation If and are two sets, then a relation between and is a triple signifying that is the domain, is the codomian, and is a set of ordered pairs with first entries from and second entries from . This triple shares the data of the sets involved and how their elements are related.
One reason relations are interesting to many people is that functions are types of relations. For more details, see my meaningful symbols, which contains notes on algebraic constructions and some theoeretic foundations.